基于环境减灾小卫星CCD数据的梁子湖水质动态监测研究

2010年武汉大学国家大学生创新实验项目

2008级 吕浩博 张翔 刘小君 张雅文

指导老师：杜娟

1       研究简介

本次科研项目基于环境与灾害监测小卫星（以下简称HJ-1A/1B）CCD数据，结合实测数据，根据梁子湖自身的特点，针对梁子湖水域的水质参数（以总氮和总磷为主），开展遥感特征信息与水体氮磷浓度的关系研究，构建水质参数遥感反演模型，并开发相应的水质遥感监原型系统，实现对梁子湖水质的长期稳定监测。

2       研究成果

2.1      预处理

 

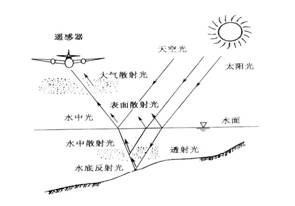
   图1 电磁波与水体的相互作用

1.辐射定标：利用ERDAS Modeler功能，按照表面附亮度计算公式L=DN/A+B和表观反射率计算公式ρ=πL* d2/(E0*cos θ) 编写模块，将HJ-1A/1B CCD数据的灰度值转换为地物反射率值以反映真实的地物特性，为定量遥感反演打下基础。

2.几何校正：利用ERDAS的Image Geometric Correction功能，以经过几何精校正的TM影像作为基准参考影像，对遥感影像进行几何精校正。结合影像的实际变形情况，纠正方法采用二次多项式，同时为了最大限度的保持原始影像的光谱信息，重采样方法采用最邻近像元法。纠正的平均误差和最大误差均小于1个像素。几何纠正采用的参考坐标系为WGS84， 投影坐标系为UTM。

3.大气校正：这是数据预处理中最困难的一个环节，多数大气校正方法还处于实验阶段。本次项目以MODIS数据作为辅助对HJ-1A/1B CCD数据进行大气校正，并利用传统的暗目标法和成熟FLAASH模型方法作为比较，分析大气校正的精度。

4.噪声去除：提取采样点附近相邻像元点平均值替代该点反射率值，达到平滑图像、消除风浪噪声的目的。

(a)大气校正前                               （b）大气校正后

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

      

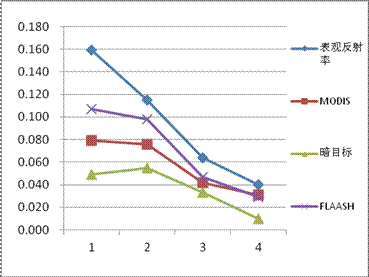
           图 2  大气校正前后梁子湖水体波谱特性曲线对比

4.1       基于遥感数据氮磷浓度反演模型研究

水体氮磷浓度遥感反演是基于不同浓度TN、TP有着不同的光谱反射率特征，即含有不同浓度TN、TP在遥感影像表现出不同的光谱反射率特性。利用卫星遥感影像，结合地面同步TP、TN浓度实测数据，利用回归统计等方法建立水体TP、TN浓度遥感监测模型，并利用该模型反演水体中TN、TP浓度，可得到氮磷浓度分布状况，从而对内陆水体氮磷浓度进行监测与预报。

 1.分析遥感数据敏感波段：在与处理之后的影像，要获取地面实测氮磷浓度与各波段以及波段组合敏感波段的分析，其原理是利用数理统计的方法，计算不同波段或者波段组合与地面实测氮、磷浓度的相关系数，然后从中选取相关系数R较大的波段或者波段组合，作为遥感数据反演氮磷浓度的敏感波段。

本次科研利用EXCEL工具对实测数据和量测数据的近70个波段及波段组合进行相关性分析，最终决定B2/B4作为总氮和总磷的相关性分析因子，相关性分别为-0.646437和0.384764。

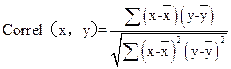（参考公式）

 2.建立氮磷浓度反演模型：

常用的检测模型有以下几种形式：

（1）线性模型

                           (3.1)

（2）对数模型

                        (3.2)

（3）指数模型

                            (3.3)

（4）一元多次项回归模型

     (3.4)

公式（3.1）（3.2）（3.3）y为氮（TN）或者磷（TP）浓度值，x为遥感波段及波段组合。公式（3.4）中y为氮（TN）或者磷（TP）浓度值，为回归系数，n为大于1的整数。

 本次科研采用半经验法以波段以及波段组合作为变量与氮磷浓度进行回归统计分析。首先选取与实测氮磷浓度相关性最大的波段或者波段组合，利用常见的几种反演模型分别建模，通过对比各个不同的反演模型，分别选取模型精度最高的成为梁子湖氮磷浓度反演模型。常见的检测模型有线模型、对数模型、指数模型、一元多次项回归模型等。

本次科研最终采用一元四次模型来构建总氮浓度的反演模型。由于总磷相关性因子的相关性较差，只有0.385，根据相关因子建立的遥感反演模型亦不能令人信服，因此本次科研并未构建总磷浓度的反演模型。

模型类型		大气校正前	大气校正后
线性模型	模型方程	Y = -0.01966x+ 0.3182	Y = -0.07758x+ 0.3973
	R2	0.0271	0.4179
	RMSE	0.09125	0.07058
一元四次模型	模型方程	Y=-0.07384x4+0.534x3-1.335x2+1.329x-0.13	Y=0.06221x4+-0.4043x3-0.8504x2 -0.7149x+0.523
	R2	0.09581	0.4991
	RMSE	0.09466	0.07046
线性模型	模型方程	Y=3.78e+012*exp(-53.71*x)0.3416*exp(-0.09889*x)	Y = -23.34*exp(0.2852*x) + 23.69 *exp(0.2809*x)
	R2	0.06725	0.4649
	RMSE	0.09371	0.07097
幂指数模型	模型方程	Y = 0.2893-1.417e-016x-29.2	Y = 0.3442-0.0163x2.458
	R2	0.08024	0.08024
	RMSE	0.08024	0.09081

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

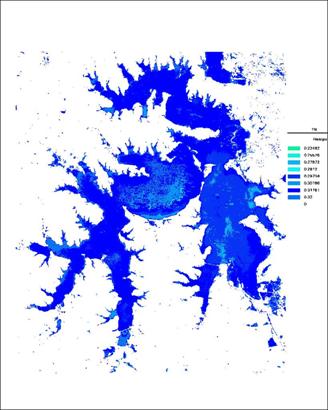
（四）基于总氮浓度可视化研究

利用ERDAS进行二次开发，在Model模块中编写程序对得到的总氮浓度分布结果进行可视化展示，并制作专题图进行输出。